查找算法

查找算法

二分查找

二分查找必须是有序对

有序的序列，每次都是以序列的中间位置的数来与待查找的关键字进行比较，每次缩小一半的查找范围，直到匹配成功。

优点是比较次数少，查找速度快，平均性能好；

其缺点是要求待查表为有序表，且插入删除困难。

因此，折半查找方法适用于不经常变动而查找频繁的有序列表。

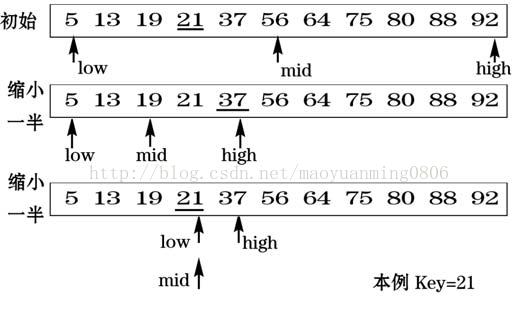
while循环实现

最好时间复杂度：O(1)

最差时间复杂度：O(logn)

空间复杂度：O(1)

/**
 * 二分查找 while实现
 * @param aar 数组
 * @param key 需要查找的元素
 * @return 所查询元素的下标
 */
fun binarySearch(aar: IntArray, key: Int): Int {
    var low: Int = 0
    var high: Int = aar.size - 1
    if (aar[low] > key || aar[high] < key || low > high) {
        return -1
    }
    var mid: Int = 0
    while (low <= high) {
        mid = (low + high) / 2
        when {
            aar[mid] < key -> low = mid + 1
            aar[mid] > key -> high = mid - 1
            else -> return mid
        }
    }
    return -1
}

递归实现

最好时间复杂度：O(1)

最差时间复杂度：O(logn)

空间复杂度：O(logn)

/**
 * 二分查找 递归实现
 * @param aar 数组
 * @param key 需要查找的元素
 * @param low 较小的下标
 * @param high 较大的下标
 * @return 所查询元素的下标
 */
fun binarySearchForRecursion(aar: IntArray, key: Int, low: Int, high: Int): Int {
    if (aar[low] > key || aar[high] < key || low > high) {
        return -1
    }
    val mid: Int = (low + high) / 2
    return when {
        aar[mid] < key -> binarySearchForRecursion(aar, key, mid + 1, high)
        aar[mid] > key -> binarySearchForRecursion(aar, key, low, mid - 1)
        else -> mid
    }
}