最近在知乎看到了一个关于洗牌算法,学习一下,记录下。
源地址:知乎:有哪些算法惊艳到了你?
问题:设计一个公平的洗牌算法
给定一个长度n个数组,最终排列的可能性一共有 n!个,公平的洗牌算法,应该能等概率地给出这 n! 个结果中的任意一个。
我们再换一个角度思考“公平”这个话题。其实也就是,对于生成的排列,每一个元素都能独立等概率地出现在每一个位置。或者反过来,每一个位置都能独立等概率地放置每个元素。
Java实现
private static Random rand = new Random();
private static List<Integer> mList = Arrays.asList(1, 2, 3, 4, 5);
public static void main(String[] args) {
List<Integer> shuffle = shuffle(mList);
System.out.print(shuffle.toString());
}
private static List<Integer> shuffle(List<Integer> list) {
for (int i = list.size() - 1; i >= 0; i--) {
// 取0-i之间的随机数
int j = rand.nextInt(i + 1);
// 交换最后一位和随机得到的数
swap(list, i, j);
}
return list;
}
private static void swap(List<Integer> list, int i, int j) {
Integer temp = list.get(i);
list.set(i, list.get(j));
list.set(j, temp);
}
Java自带API
在Java提供的Collections包中,提供了shuffle方法
Collections.shuffle(mList);
看下源码:

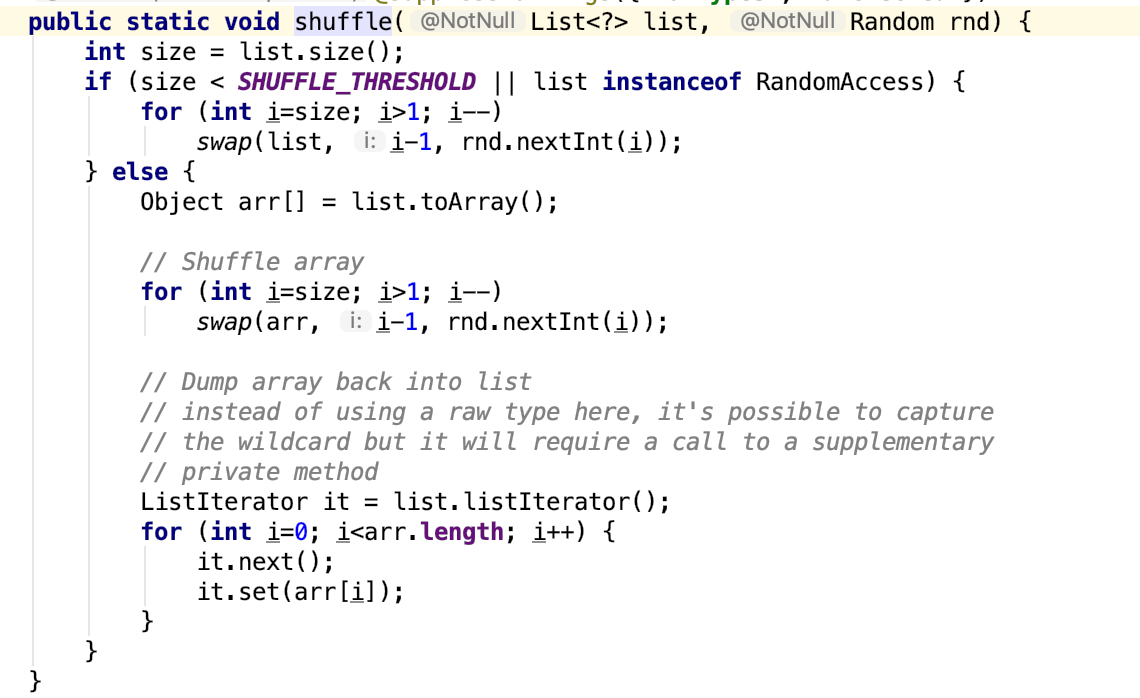
可以看出,和上面的思路一样
思路解析,参考上面的链接,知乎的原答案
比如数组1,2,3,4,5
我们从后往前
先取任意1个元素和最后一个交换位置,那么任意一个元素出现在数组最后面的概率为1/5
我们继续,取任意一个元素和倒数第二个交换位置,概率为4/5*1/4=1/5
依次类推,每一个元素出现在每一个位置的概率,都是 1/5
遍历时,为什么采用从后到前的方式,而不采用从前到后?
因为生成 [0, i] 范围的随机数比生成 [i, n) 范围的随机数简单
- 生成[0, i]范围的随机数
Random rand = new Random();
int randNum = ran.nextInt(i + 1);
- 生成[i, n)范围的随机数
Random rand = new Random();
int randNum = rand.nextInt(n - i) + i;